Parallel Resistor Calculator

Table of contents:

Parallel resistor formula
How to calculate parallel resistor
How to use the calculator
FAQs

Parallel resistor formula

The formula to calculate the equivalent resistance of resistors connected in parallel is 1/R = 1/R₁ + 1/R₂ + ... + 1/R_n.

\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + ... + \frac{1}{R_n}

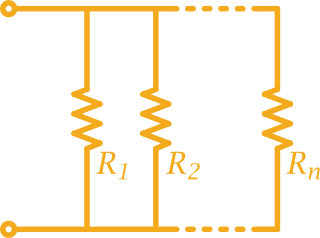
Where R is the equivalent or total resistance value of the parallel circuit and R₁, R₂, ...R_n is the resistance value of each resistor.

How to calculate parallel resistor

When you connect resistors in parallel, each component has the same voltage source or shares the same voltage. Depending on each resistor's resistance value, the amount of current that flows through them can be found using Ohm's law formula.

${I_1}=\frac{V}{R_1},{I_2}=\frac{V}{R_2}, ... , {I_n}=\frac{V}{R_n}$

So the total current generated by the power source is the sum of all current combined.

${I}={I_1}+{I_2}+...+{I_n}$

${I}=\frac{V}{R_1}+\frac{V}{R_2}+ … +\frac{V}{R_n}$

${I}={V}(\frac{1}{R_1}+\frac{1}{R_2}+ … +\frac{1}{R_n})$

Alternatively, we can calculate the total current using the equivalent resistance connected to the power source.

${I} = \frac{V}{R}$

${I} = {V}(\frac{1}{R})$

We can now find the equivalent resistance using the following formula.

$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + ... + \frac{1}{R_n}$

Example: Calculating equivalent resistance of a parallel circuit

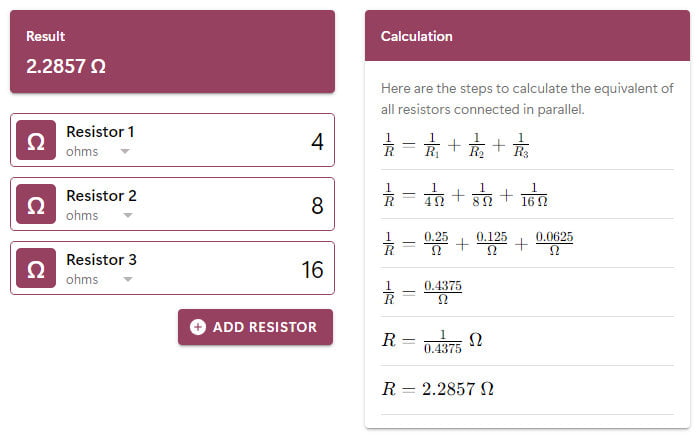
What is the total resistance of a connection consisting of three resistors: ${R_1} = {4.00 Ω}, {R_2} = {8.00 Ω},$ and ${R_3} = {17.00 Ω}$?

To find an equivalent resistance of the parallel resistors in the connection, use the following formula and follows by entering the given values.

$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$

$\frac{1}{R} = \frac{1}{4.00 Ω} + \frac{1}{8.00 Ω} + \frac{1}{17.00 Ω}$

Therefore,

$\frac{1}{R} = \frac{0.25}{Ω} + \frac{0.125}{Ω} + \frac{0.0625}{Ω}$

$\frac{1}{R} = \frac{0.4375}{Ω}$

${R} = \frac{1}{0.4375}{\ Ω}$

${R} = {2.2857\ Ω}$

The total resistance of the current connection with three resistors is ${R} = {2.2857\ Ω}$.

How to use the calculator

Our parallel resistor calculator calculates the equivalent resistance in real-time as you enter or change each resistor's value. It is responsive and works on either desktop or mobile.

The calculator starts with two input boxes for two resistors, and you can add as many as you like by using the Add Resistor button.

You can also change the individual resistance unit from Ω (ohms) to mΩ (milli-ohms), kΩ (kilo-ohms), and MΩ (mega-ohms) by using the drop-down menu next to each box.

The result will appear in two places. The Result section will show only the final value of the equivalent resistance of the parallel circuit, while the Calculation section will show you the detailed steps.

Parallel Resistor Calculator Example — Using the calculator to find the result

FAQs

1. Why the equivalent resistor is always lower than the individual resistor in a parallel connection?

When you add a new resistor, it makes a new path that the current can flow through. So the current flows from the source are always higher than the individual resistor. According to Ohm's Law, with the same voltage, higher current means lower resistance.

2. Are all resistors in parallel share the same voltage?

Yes, they are! Because in a parallel circuit, all resistors are connected directly to the voltage source.

Parallel Resistor Calculator Explained

Parallel resistor formula

How to calculate parallel resistor

How to use the calculator

FAQs

Parallel Resistor Calculator App